最近マイクラの記事ばかり書いていて、「学生成分が足りていないのでは…」と思ったので学生らしく? C言語を使用して、数値積分をやってみました。
1. 考え方
積分の証明は調べれば出てくるので、考え方だけ簡単にまとめます。
- ある関数を分割していき、短冊状にする
- 短冊状になった長方形の面積を計算する
- その面積を足し上げていけば面積が求まる
たったこれだけです。図にするとこんな感じです。
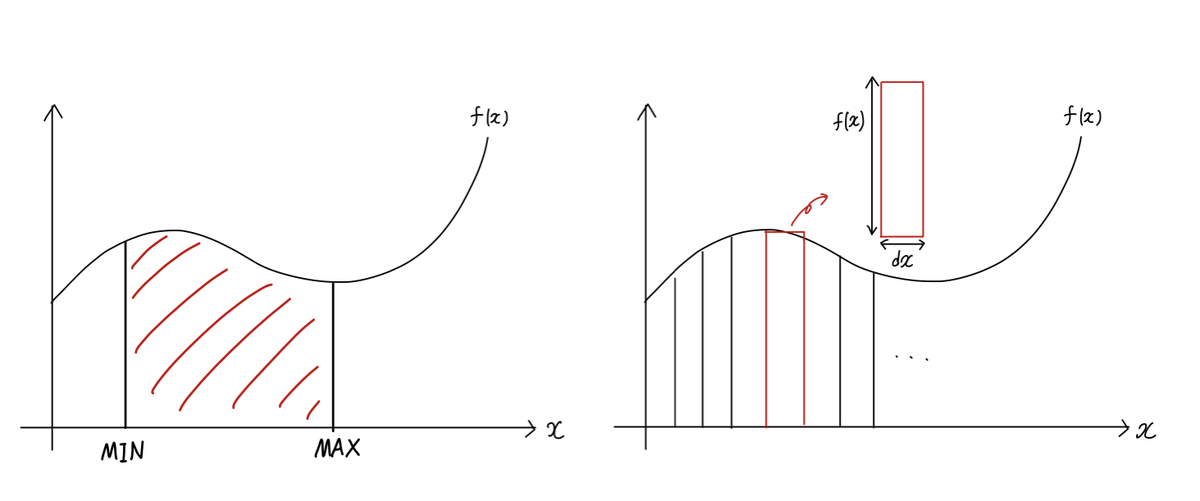
1.1 短冊1つあたりの底辺の長さ
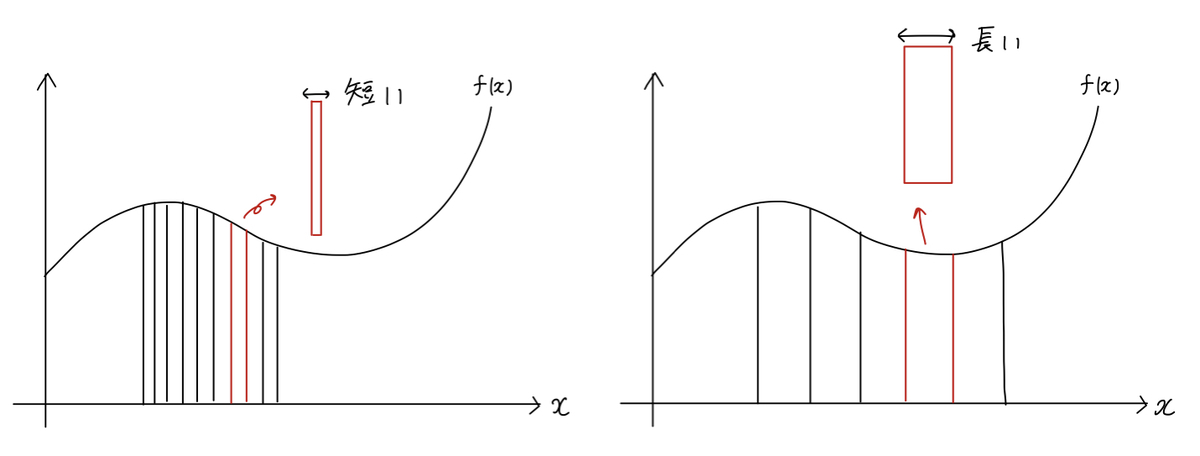
底辺の長さ は、分割数
によって変わります。分割数が多いほど短くなり、分割数が少ないほど長くなるので
と
は反比例の関係です。
また、底辺の長さは積分区間 [MIN, MAX] そのものなので、それを分割すると考えれば
となります。これが底辺の長さです。
1.2 短冊1つあたりの高さ
高さ(大きさ) は、底辺の位置
番目によって変わります。なので、底辺の位置(長さ)
を
に代入することで、短冊の高さを求めることができます。つまり、
となります。
1.3 短冊1つあたりの面積
短冊の底辺の長さが 、短冊の高さが
になので、面積は底辺×高さで
となります。
1.4 求める面積
求める面積は、積分区間 [MIN, MAX] とすると、短冊の面積をその区間分だけ足し上げていけばいいので
となります。総和は for 文を使用すれば実装できます。
積分範囲は 0 からはじまるとは限らないので、その分のズレを含めると に代入する変数は
になります。なので、C言語にすると
int val[DIV]; int i; //分割した数だけ for を回す for (i = 0; i < DIV; i++) { //その位置における短冊の面積 = 高さ×底辺 val[i] = function(MIN + i * dx) * dx //短冊1つあたりの面積を総和 -> 積分区間の面積 surface += val[i] }
となります。
2. 実装例
ここまでを踏まえて、プログラムを書いていきます。今回は、コンソール出力だけでなく CSV 形式のファイル出力を行う機能も追加しました。CSV 形式のファイルを Ngraph や Excel などで読み込むと、簡単にグラフを描画できるので便利です。
求めたい関数は function の return 部分に書き込みます。
#include<stdio.h> #define MIN -5.0 #define MAX 5.0 #define DIV 100 //計算したい関数 double function(double x) { return x*x; } int main() { FILE *fp; char *file_name = "surface.csv"; //分割した短冊1つあたりの底辺 double dx = (MAX - MIN) / DIV; //短冊1つあたりの面積 double val[DIV]; //積分した結果 double surface; int i; for(i = 0; i < DIV; i++) { //短冊の高さと底辺の積 val[i] = function(MIN + i * dx) * dx; //短冊の面積の総和 surface += val[i]; } //ファイルオープン fp = fopen(file_name, "w"); if(fp == NULL) { printf("file could not be opened."); return -1; } //ファイル書き込み for(i = 0; i < DIV; i++) { fprintf(fp, "%lf,", MIN + i * dx); fprintf(fp, "%lf", val[i]); fprintf(fp, "\n"); } fclose(fp); printf("surface = %lf", surface); return 0; }
2.1 三角関数の場合
三角関数を使用するには math.h を使用しますが、sin() や cos() などの引数には弧度法による値を入れる必要があるので、度数法から弧度法に変換する関数をはさみます。また、Visual Studio Code では M_PI 定数を使用するために _USE_MATH_DEFINES を定義する必要があるようです。
#define _USE_MATH_DEFINES #include<stdio.h> #include<math.h> #define MIN 0.0 #define MAX 360.0 #define DIV 100 double function(double x) { return sin(x); } double deg2rad(int deg) { return deg * (M_PI / 180); } int main() { FILE *fp; char *file_name = "surface.csv"; double dx = (MAX - MIN) / DIV; double val[DIV]; double surface; int i; for(i = 0; i < DIV; i++) { //三角関数の場合は弧度法に変換する関数をはさむ val[i] = function(deg2rad(MIN + i * dx)) * dx; surface += val[i]; } fp = fopen(file_name, "w"); if(fp == NULL) { printf("file could not be opened."); return -1; } for(i = 0; i < DIV; i++) { fprintf(fp, "%lf,", MIN + i * dx); fprintf(fp, "%lf", val[i]); fprintf(fp, "\n"); } fclose(fp); printf("surface = %lf", surface); return 0; }
3. 実行結果
3.1 二次関数
まずは1番目の実装例である二次関数のCSVデータを Ngraph を用いてグラフ化したものです。積分区間は [-5, 5]、分割数は 100 です。
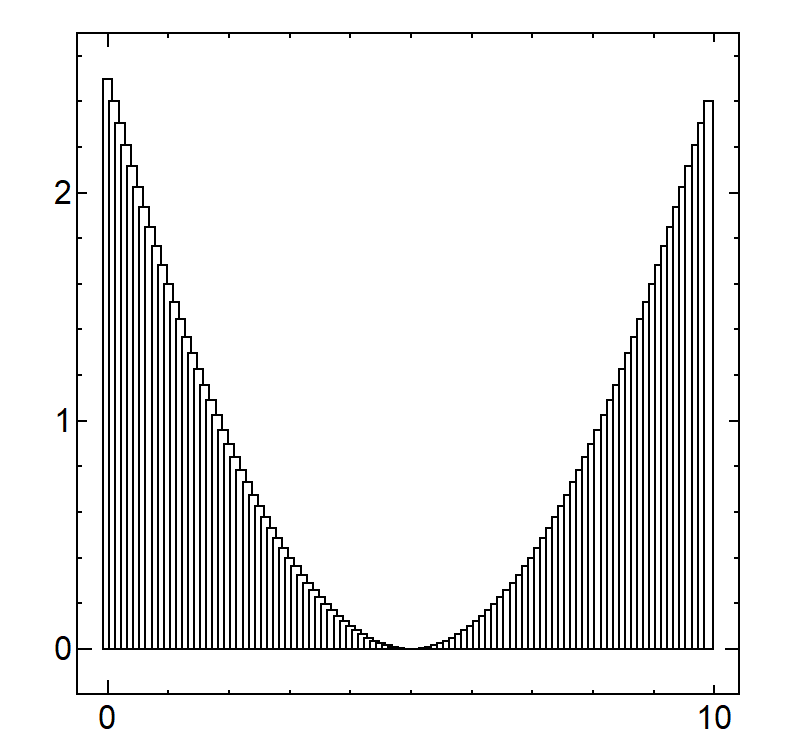
3.2 Sin 関数
次に、2番目の実装例である Sin 関数をグラフ化したものです。積分区間は [0, 360] ([0, 2])、分割数は 100 です。
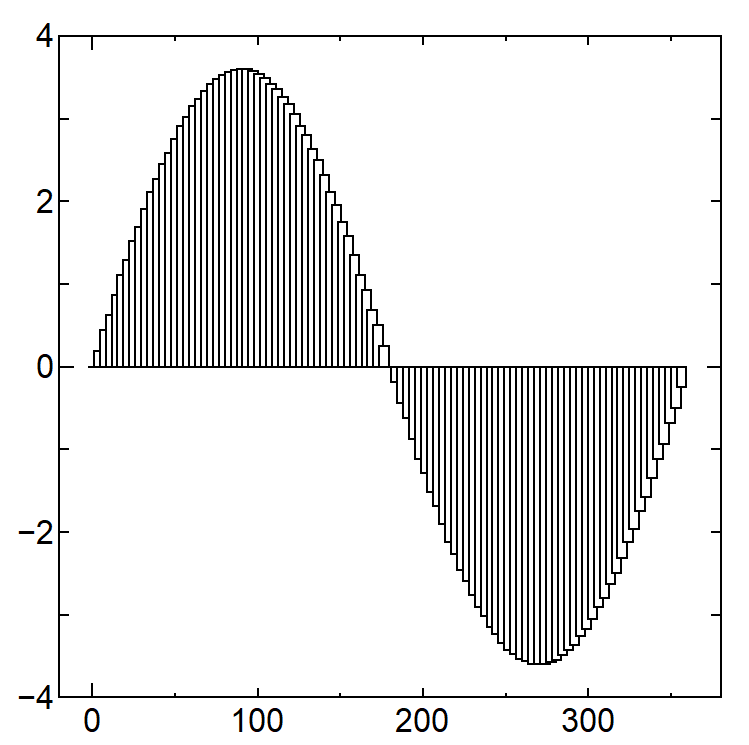
3.3 分割数を変えたときの変化
DIV の定義部分を 10, 50, 100, 200, 500 と変えていったときの違いです。短冊の分割数を多くするほど、精度は良くなります。
関数は
【分割数 10 / 面積 89.28】
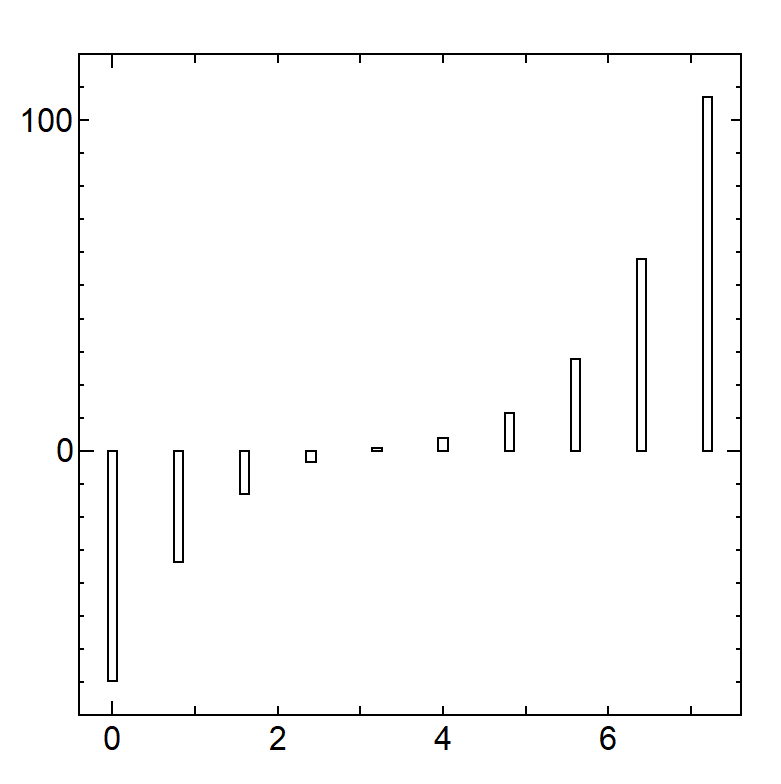
【分割数 50 / 面積 185.8432】
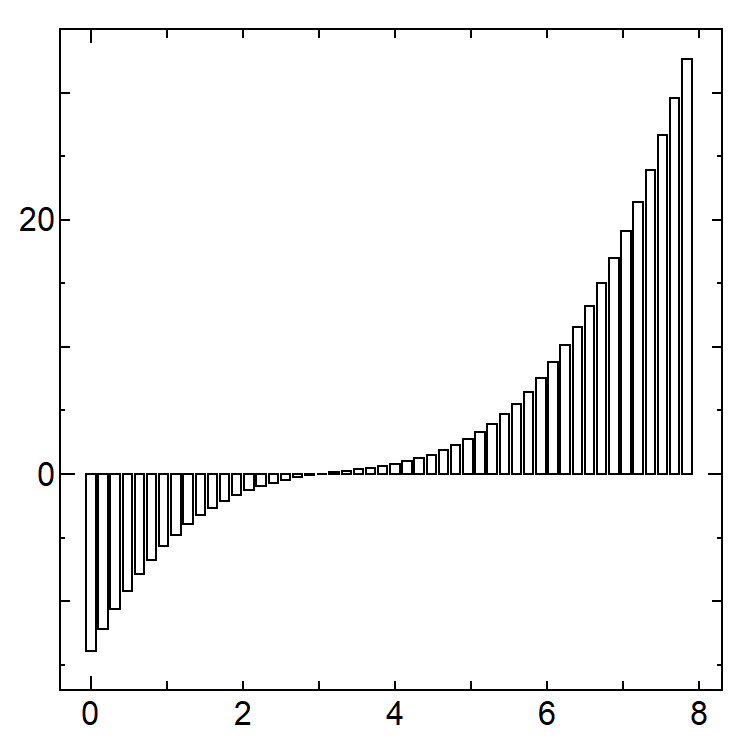
【分割数 100 / 面積 198.2208】
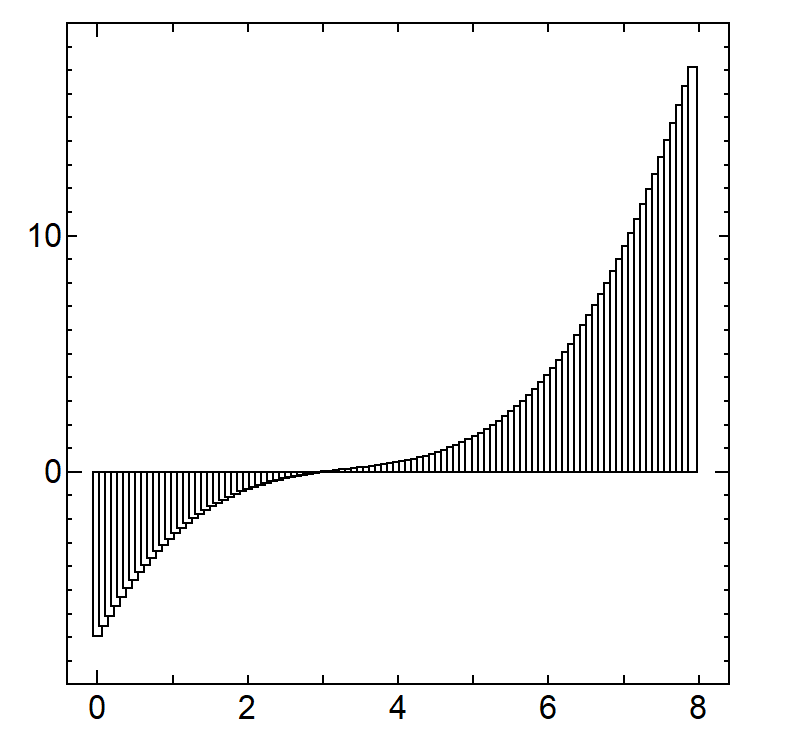
【分割数 200 / 面積 204.4352】
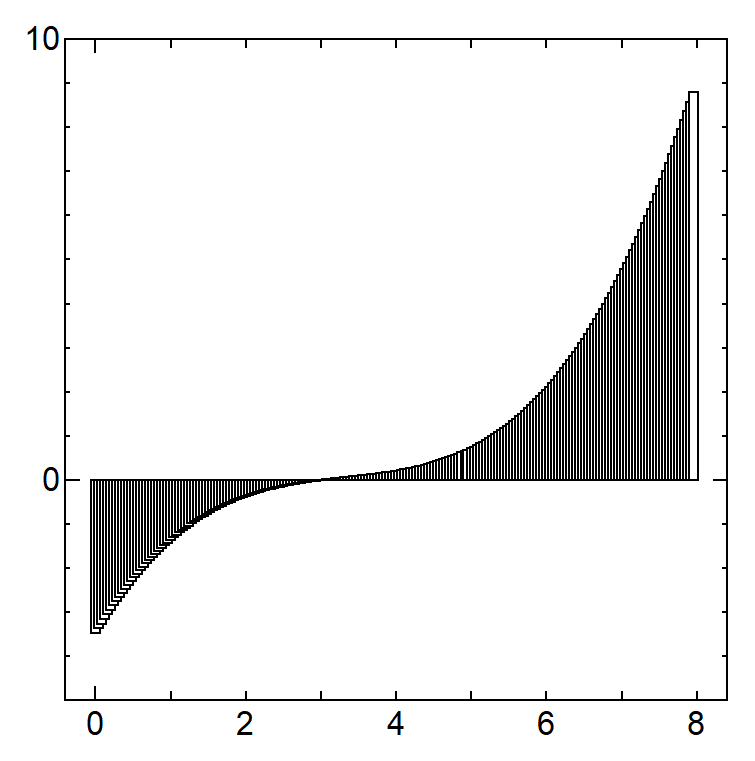
【分割数 500 / 面積 208.172032】
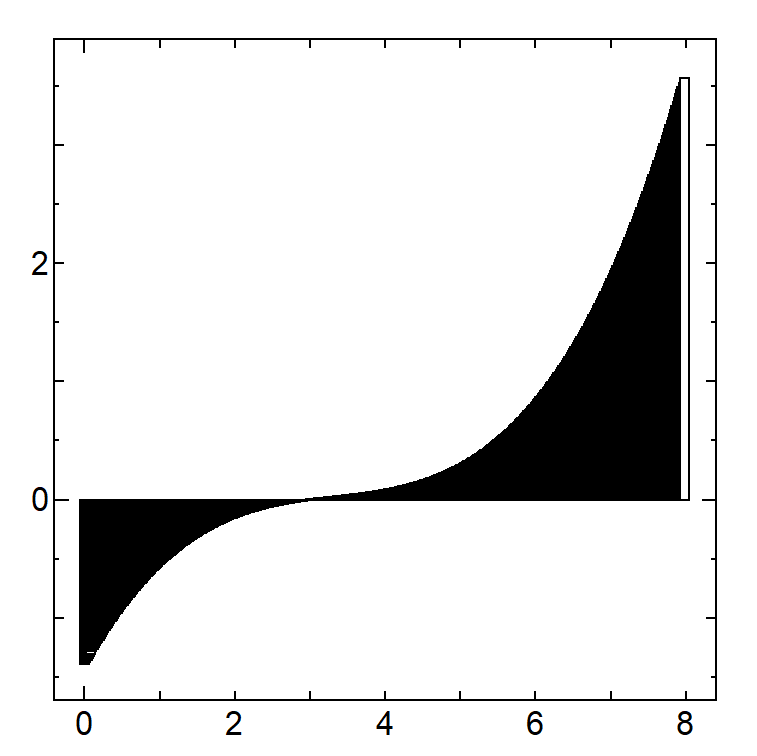
ちなみに、Wolfram Alpha で計算すると面積は約 210.67 になるので、もっと分割数を増やせばこの値になります。
ぜひ、いろんな関数で試してみてください!
イベントのお知らせ
2021年10月31日(日曜日)に、MS Tech Camp 1周年記念イベントを行います!
MS Tech Camp シリーズのイベントでは、Microsoft Azure や Github, Minecraft などを用いたハンズオンを行ってきました。今回はゲスト登壇や、MS Tech Camp でやってきた内容の総まとめライブコーディングなどを行う予定ですので、お気軽にご参加ください!
当日は Youtube Live での配信予定です。
