光や電子という、世界の根源的な存在に目を向けたとき、それは粒子と波動という一見矛盾した2つの性質を同時に成り立たせていることがわかってきました。
しかし、古典物理学ではその振る舞いを説明することができません。
放射線や線スペクトルの問題から、物理学者たちは原子の内部がどんな構造になっているかに興味の対象を広げていきました。
しかし、原子の内部構造を考え始めると、原子核やその周りに存在する電子の振る舞いは、やはり古典物理学では成立させることができませんでした。
ニュートン以来、世界を支配する盤石な学問だった物理学は、ここで大きな壁にぶつかったのです。
物理学者たちはもはや、使い慣れた古典物理学には別れを告げ、新しい事実に対応した新理論を作るしかなかったのです。
しかしこうして生まれた量子力学には、さまざまな奇妙な性質がありました。
「物事は確率でしかわからない」「観測するまで物事の状態は確定しない」という不可思議な理屈や、「シュレーディンガーの猫」と呼ばれる哀れな猫の思考実験、そしてアインシュタインの「神はサイコロを振らない」という言葉。
そんな誰もが聞き慣れた不思議な量子力学の議論はすべて、エルヴィン・シュレーディンガーの波動方程式が登場してから、その解釈を巡って始まります。
そして、この問題は、共に量子力学の誕生に貢献してきたアインシュタインとボーアを対立させ、議論を戦わせる原因になるのです。
彼らは量子力学の何を受け入れ、何を拒んだのでしょうか?
目次
- 2つの量子力学
- シュレーディンガー方程式は一体何を計算しているのか?
- それは存在確率の波
- ハイゼンベルクの不確定性原理
- コペンハーゲン解釈
2つの量子力学
物理学において重要な課題の1つが、実験結果と一致した値が導ける方程式(法則)を見つけ出すことです。
しかし、粒子と波動という相容れない2つの性質を示す光や電子の振る舞いは、古典物理学の常識では説明できず、実験と一致した値を計算することもできませんでした。
そこで、ハイゼンベルグは新しい理論「行列力学」を作り出し、これを計算できるようにしました。
これはざっくり言えば、電子の振る舞いについて、取りうる値を全部書き出して行列計算するというものです。
しかし当時の物理学者たちにとって、行列計算はまったく馴染みのない計算方法でした。
しかも数学が得意だったハイゼンベルクは「別に視覚的なイメージが伴わなくても何の問題もないだろう」と考えていたため、ここまでの解説で多用したような、図に描いて解説できるイメージが何もありませんでした。
今記事を読んでいる読者も行列力学が何なのかほとんど意味がわからないでしょうが、実際当時の物理学者たちもこの理論がどんな現象を取り扱っているのかさっぱりわからなかったのです。
物理学は数学とは異なり、目に見える現実の現象を取り扱った学問です。
そのため、現象をイメージもできず、難解な計算方法を強いる行列力学は、物理学者たちもうんざりだったのです。
そんな中、救世主のごとく登場したのが、現代でも誰もがその名を知るエルヴィン・シュレーディンガーです。

シュレーディンガーは、幅広い分野をカバーできる器用な理論家で、他人の研究を分析してわかりやすく解説する能力に長けていました。
あるときシュレーディンガーはアインシュタインの論文の中で引用されていた、ド・ブロイの学位論文を見て興味をもちます。
ド・ブロイの理論は先に説明したように、電子などの物質も光同様に波として振る舞うと主張したもので、その波は物質波(ド・ブロイ波)と呼ばれていました。
シュレーディンガーはこの理論についても、見事な解説を行います。
しかし、その解説を聞いた物理学者のピーター・デバイは「ド・ブロイの理論には物質波を記述する波動方程式が存在しないからナンセンスだ」と指摘しました。
それはシュレーディンガーから見ても、もっともな意見でした。波動方程式がない波の理論など、物理学では話にならないからです。
そこでシュレーディンガーはド・ブロイの言う物質波を記述する波動方程式について考えてみました。
最初シュレーディンガーは特殊相対性理論と矛盾しない波動方程式を考えていましたが、それは実験結果と一致した答えを導けませんでした。
そこで彼は古典物理学の常識は無視して、物質波の波長と、粒子の運動量を結びつける方程式を創作したのです。
そうして誕生したのが、かの有名なシュレーディンガー方程式です。
この波動方程式を基礎にして、シュレーディンガーは新理論『波動力学』を打ち立てます。
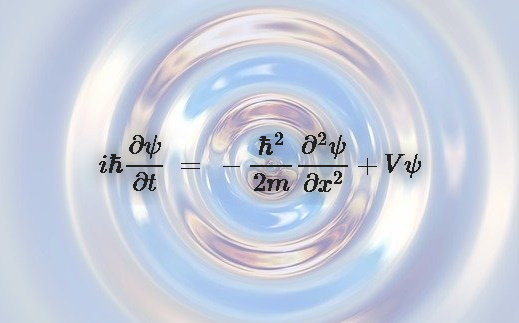
余談ですが、シュレーディンガーはとっかえひっかえ愛人を作るプレイボーイで、この世界に革命を起こす偉大な波動方程式を見つけ出したのも、不倫旅行の最中でした。
そのため、ボルンには「彼のような私生活は私たちのような平凡な人間には理解できない」と言われ、ドイツ人数学者のヘルマン・ヴァイルにはこの偉業を「人生後半のエロスの噴出の賜物だ」、と言われたそうです。
そんなシュレーディンガーの私生活の問題はともかくとして、ハイゼンベルクの行列力学に苦しんでいた物理学者たちは、この波動力学に「待ってました!」とばかりに飛びつきました。
なにせこの理論は謎めいた行列とは異なり、電子の振る舞いを馴染み深い波のイメージで視覚的に説明してくれた上、計算に必要な技術は物理学者たちにとって非常に使い慣れた微分方程式でよかったからです。
これにはプランクもアインシュタインも称賛を贈り、ゾンマーフェルトさえ「行列力学が正しいことは疑う余地がないが、取り扱いが非常に難しく、恐ろしく抽象的だ。シュレーディンガーはそこから我々を救ってくれた」と評しました。
パウリもその明快さに驚愕し感銘を受けたと語り、行列力学の誕生に貢献したボルンさえ波動力学に乗り換えてしまいました。
面白くないのはハイゼンベルクでした。
彼からすれば、突然お株を奪われたようなもので、しかも盟友のパウリにも、師であるボルンにも裏切られたと感じたのです。
ハイゼンベルクは原子レベルの出来事を正しく記述しているのは自分のほうだと考えていました。
しかし、正しいも何も、不思議なことにまったく形式の異なるこの2つの理論は、同じ問題に当てはめた場合、まったく同じ結果を出すのです。
波動方程式を使い波を記述する理論と、行列代数を使い粒子の状態を書き出した理論が、数学的には等価なものだったのです。
この事実はイギリス人の理論物理学者ポール・ディラックによって証明されます。
それは波動と粒子の二重性に、再び直面する問題でした。
シュレーディンガー方程式は一体何を計算しているのか?
物質波を計算する波動方程式を見つけ出し、一世を風靡したシュレーディンガーでしたが、彼自身わかっていない問題がありました。
それはシュレーディンガー方程式が具体的には現実の何の波を計算しているのか? ということでした。
シュレーディンガーの波動方程式は、波動関数ψという波の、ある時刻tにおける、任意の点xの波の形を教えてくれます。
しかしシュレーディンガー自身、この波動関数ψが何を表しているのかわかりませんでした。
波といっているけれど、それは一体何が波打っているんだろう? それはシュレーディンガーを含め、みんなの疑問でした。
水の波は、上下運動する水分子の集団的な動きです。音波も、それは空気中の分子が波打って伝わっているものです。
波はその運動を伝える媒質が存在しなければ成り立ちません。
しかし、シュレーディンガー方程式の計算する物質波は、電子1つの波という古典物理学的な理解では意味不明なものを計算しています。
シュレーディンガーはこれを「電子の電荷が雲のように広がったものだ」という解釈をしました。
波動方程式が表しているものは、ある時刻tの任意の場所xにおける電荷の密度だ、というのが彼の考えでした。
では、数々の実験結果が示す粒子としての電子はなんなのでしょう?
シュレーディンガーはこれを、物質波のピークになった部分を我々が粒子と捉えているだけだと説明しました。
物質波は空間の至るところへ広がって、さまざまな波長の波が干渉を起こしています。それは束ね合わさって波束を作ります。その波束のピークが我々には粒子に見えるのだというのです。
あろうことかシュレーディンガーは、物質波を成立させるために、粒子なんて本当は存在しないと主張したのです。
しかしこの理屈だと、波のピークはいくつもできるので、1つの電子が2つや3つに分裂して観測されても良いということになってしまいます。
どうして電子は1つのポイントに収束するのでしょう?
さらに、波動関数には、水素のような電子1つの場合はいいけれど、ヘリウムのように電子2つを含んだ原子の場合、3次元空間に2つの波があるという記述にならず、次元を足し合わせて6次元空間に存在する1つの波として記述してしまうという性質がありました。
これは電子が原子内に1つ増えるたびに、計算する次元が3つ増えるという恐ろしい状態を作り、ウランの波動関数に至っては276次元空間の波という記述になるのです。
これは物質波がシュレーディンガーの期待したような明快な実在の波ではなく、非常に抽象的な多次元空間の波であることを示していました。
それにシュレーディンガーの説明では、結局粒子性の証拠であるプランクの放射法則も光電効果もコンプトン効果も説明できないのです。
そのため、ボルンにも「シュレーディンガーの偉業は結局数学なのであって、彼の物理学はかなりお粗末だ」と言われてしまいます。
しかし、シュレーディンガーの波動関数が実在の三次元空間の波でないのだとしたら、この波は一体何を表しているのでしょうか?
マックス・ボルンは、この問題に対して、歴史に名を残す重要な解釈を提唱します。
それは、波動関数の確率解釈と呼ばれるものでした。
それは存在確率の波
いろいろ無理のあったシュレーディンガーの解釈に代わってボルンが考えたのは、波動関数が抽象的な可能性を表しているというものでした。
広がる波を計算している以上、波動関数からは電子の実際の位置は得られません。
では、我々は一体何を計算しているのかと言うと、それは電子がどこで見出されるかという確率なのだとボルンはいうのです。
ある地点Xとある地点Yで、波動関数を計算したとき、Yの方が値が大きいとすれば、それはYで電子が見出される可能性が高いことになります。
しかし、電子はXで見出されるかもしれないし、YでもXでもない場所で見出されるかもしれません。
シュレーディンガーの計算していた波とは、物理的に実在するものではなく、そこに電子があるかもしれないという存在確率の分布だとボルンは主張したのです。
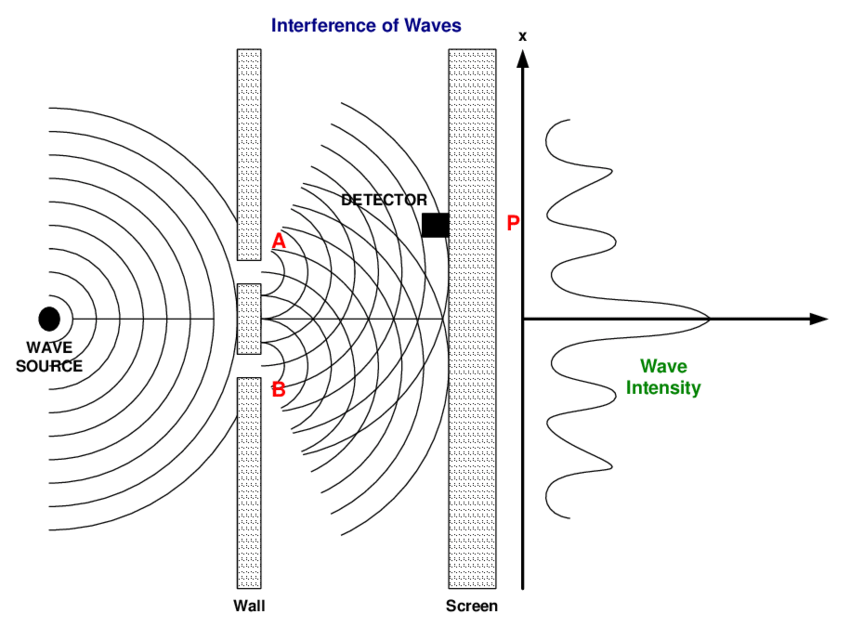
しかし、これはシュレーディンガーにとっては受け入れがたい解釈でした。
物理学の世界は基本的に因果律に支配された決定論で記述されています。
例えばビリヤードで白ボールを別のボールにぶつけた場合、どのくらいの力でどの角度からぶつけたかによって、ボールが弾かれる方向と勢いは決まっています。
しかし、ボルンの解釈を当てはめてしまうと、ボール同士をぶつけたときに、どちらの方向へどのくらいの勢いで弾かれるのかは、確率でしか言及できず、いずれの状態になるか事前にはわからないことになるのです。
そんな馬鹿なことがあるわけない、というのがシュレーディンガーの考えでした。
なにより、せっかく自分が抽象的な電子の振る舞いを、連続して滑らかにつながる物理的な波として視覚的に表現し直したというのに、ボルンは再びそれを不連続で抽象的なものに戻してしまったのです。
そして、この確率解釈については、シュレーディンガー同様、納得していない人物がいました。それがアインシュタインです。
因果律と決定論を放棄する確率解釈は、アインシュタインにとってもありえないものでした。
だから彼はこういったのです。「神はサイコロを振らない」と。
ここから、量子力学は世界でもっとも成功した理論と言われながらも、その解釈を巡っては物理学の偉人たちが真っ向から対立し合う、奇妙な戦国時代に突入していくのです。
ハイゼンベルクの不確定性原理
解釈の仕方はどうあれ、世間の流れは完全にシュレーディンガーの波動力学に向いていました。
しかしそんな中、ハイゼンベルクはなんとか自分の行列力学を復権させようと頑張っていました。
あるときハイゼンベルクは、ベルリン大学でアインシュタイン、ラウエ、プランクといったそうそうたる顔ぶれの前で、行列力学の講演を行う機会を得ます。
この時点で若干25歳だったハイゼンベルクは、ひどく緊張したことでしょう。
アインシュタインは、「君の仮定はおそらく正しいだろう」としながらも、視覚的な電子の軌道を認めないハイゼンベルクの考え方に、「なんでそんなおかしなことを言い出すのか?」 と尋ねました。
これに対してハイゼンベルクは、我々は直接観測可能な量だけに基づいて考えるべきだと主張します。
しかし、アインシュタインはハイゼンベルクの「観測可能な量だけで理論を作る」という考えを否定します。
なぜなら、アインシュタインに言わせれば「何が観測可能かを決めているのは理論のほう」だからです。
何が観測可能かという問題は、ハイゼンベルクの理論の仮説に過ぎず、その考えに則って君は結果を見ているだけだ、とアインシュタインは言うのです。
この指摘にハイゼンベルクは意表をつかれ、よく考えてみるべき問題だと感じました。
またこの頃、ハイゼンベルクにとっては、もう1つ難しい問題が登場しました。
それがスコットランド人の物理学者ウィルソンが発見した霧箱の問題です。
霧箱というのは、過飽和状態の蒸気を満たした箱のことです。
ここに放射線を放つと空気分子が電離して、そのイオンを核に蒸気が凝結し、荷電粒子の軌跡が飛行機雲のように見えるのです。

波動力学では電子や光子は波であり空間をどんどん広がるので直線の経路など持ちません。
一方行列力学の考え方でも、電子などに移動の軌跡は存在しないはずでした。
電子や光に「粒子と波」という2つの性質を持たせるためには、明確な経路を持って移動しないというのは重要なポイントだったのです。
ハイゼンベルクの考えでは、電子は量子飛躍という突然ぴょんと別の場所にジャンプして移動するおかしな挙動をするものだったのです。
シュレーディンガーはこの考えを嫌って、波としての表現を主張しました。
しかしハイゼンベルクにとって量子飛躍は、絶対に外すことのできない量子力学の重要な性質だったのです。
では霧箱に見える軌跡は一体なんなのでしょう? これは本当に電子の軌跡を表しているものなのでしょうか?
ハイゼンベルクは、考え抜いた末に、この飛行機雲のような軌跡が電子の正確な位置を表すものではなく、だいたいの位置を示すものでしかないということに気づきます。
「これはぼんやりした点の並びに過ぎず、見ているものは電子などより遥かに大きい水滴の列だ」
つまり、霧箱の中で軌跡のように見えるものは、シュレーディンガーの理論で言えば波束が鋭い波でしかなく、粒子が通る明確な直線の軌跡ではないのです。
では抽象的な概念を好むハイゼンベルクは、この事実をどのように理解したでしょうか?
彼は、これが電子に関する情報の不確かさなのだと考えました。
「何が観測可能で、何が観測できないのか? それはどうやって決まっているのか?」
ハイゼンベルクはこのとき、アインシュタインの何が観測可能か決めるのは理論だという指摘を思い出します。
そして彼はここから、運動量と位置の情報が同時には得ることができず、両者には不確定性がつきまとうという、量子力学でも特に重要な理論、ハイゼンベルクの不確定性原理を発見するのです。
もし電子に軌跡があるのだとすれば、それはある時間ごとの電子の位置qを連続して観測していくことに他なりません。
しかし、電子のように小さな粒子は、なんらかの粒子との干渉で観測を行った場合、あらぬ方向へ弾き飛ばされてしまって、もともと持っていた運動量を失ってしまいます。
これでは瞬間的な位置を知ることはできても、その後の経路はめちゃくちゃになって意味を持たなくなるでしょう。

行列力学では、粒子の運動量pと位置qの順番を入れ替えて掛け算すると、答えが変わってしまうという非可換性を持っていました。
行列力学の発見当時、その理由をハイゼンベルクは説明できませんでしたが、これは運動量を測定してから位置を測定した場合と、位置を測定してから運動量を測定した場合では、観測結果が変わってしまうことを意味していたのです。
つまりは、私たちは電子について、運動量と位置を同時に知ることは禁じられていたのです。
そのため、後にハイゼンベルクは、この理論の名前は「不確定性」と呼ぶよりは、「不可知性」と呼んだほうがよかったかもしれないと言っています。
このような測定の曖昧さは、電子に明確な軌道を持たせることを禁じています。
だから、電子は空間の中でつながった経路という古典物理学的な概念を持たなかったのです。
コペンハーゲン解釈
ここまでの説明を聞いて、なんだか釈然としない、と感じた人は多いのではないでしょうか?
その理由はおそらく、光や電子が波と粒子という両方の性質を持つといいながら、いずれの理論も光や電子を波か粒子のいずれかで捉えて説明しているためでしょう。
実際、多くの物理学者が、この点についてなんとも釈然としない思いを味わっていました。
それはボーアも同様でした。
ボーアはこのとき、シュレーディンガー方程式と行列力学が数学的に等価であり、波動と粒子の二重性が同時に成り立つという量子力学の不思議な問題について考えていました。
そのためハイゼンベルクが、不確定性原理のアイデアを論文として発表させてほしいと許可を求めてきたとき、「この理論は多分正しくないから発表しない方がいい」と、拒否してしまったのです。
ハイゼンベルクの理論はあくまで電子を粒子として捉えていました。
不確定性原理についても、小さな電子にガンマ線などの別の粒子を衝突させることで発生するという説明の仕方をしていたのです。
けれど、ボーアにとって電子や光子の二重性はもはや除外することのできない問題でした。
電子の振る舞いは、粒子か波動かのどちらかを選択したのでは説明できないと直感的に理解していたのです。
しかし、ハイゼンベルクにとって不確定性原理は自信作の理論でした。そのため彼は悔しさのあまり、ボーアの目の前でぽろぽろ泣き出してしまったといいます。
せっかく良いアイデアがあるのに、上司が分からず屋で許可をくれない、という悩みを経験した人は多いかもしれませんが、このときのハイゼンベルクもそんな気分だったのでしょう。
しかしボーアが、シュレーディンガーの波動方程式を取り入れることで、不確定性のいくつかの問題が説明可能になることを示すと、ハイゼンベルクもそれを認めざるを得なくなりました。
正直ハイゼンベルクはシュレーディンガーの理論を取り入れることは気に入らなかったのですが、そこは妥協して修正した論文を発表します。
結果的にこの論文は非常に高く評価され、ハイゼンベルクは正教授の職を得て、コペンハーゲンの研究所を後にすることになります。
ちょっとしたしこりを残して、研究所を去る事になったのでハイゼンベルクは、ボーアに恩知らずな印象を与えなかったか気にしていました。
でも、ボーアはハイゼンベルクの才能も不確定性原理も高く評価していて、彼のことを褒めながらアインシュタインに意見を求める手紙を書いていたくらいなので、心配は無用だったでしょう。
その後ボーアは、「相補性」という自らのアイデアを核にして、波動と粒子という二重性の問題を1つにまとめようと奮闘します。
相補性とは、全く相容れない波動と粒子の性質のどちらか一方しか我々には見ることができないが、電子と光子はその両方の性質を排他的かつ相補的に持っているという考え方です。
これはどういった観測の仕方をするかが、電子の波動、粒子いずれかの性質を決定するという考え方でした。
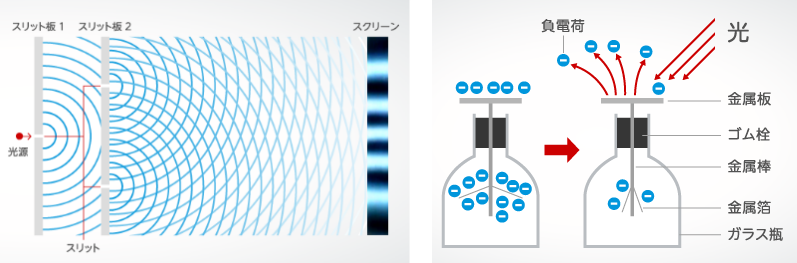
ボーアはこの電子などが持つ、排他的かつ相補的な関係を同時に観測できないのは、自然界に備わった限界なのだと説明しました。
このアイデアを聞いたハイゼンベルクは、あまり納得がいかなかったようで「あんな考え方でいいなら、矛盾なく説明できるのは当然だろう」とパウリに愚痴ったといいます。
しかし1927年、ボーアはこの相補性の考えをまとめた最終的なアイデアを、イタリアで開催された国際物理学会で初めて公式に発表します。
それは、不確定性原理やシュレーディンガー方程式、ボルンの確率解釈など、これまでの量子力学研究で発見されたさまざまなアイデアを全て取り入れた、到達点と呼ぶべきものでした。
しかし、これを聞いた物理学者たちは、ハイゼンベルクを含め、皆が戸惑ってしまいます。
それは非常に驚くべきことを主張していました。
このときボーアが語った複雑な考えは後に「コペンハーゲン解釈」と呼ばれることになります。
これは現代の我々にとっても、非常に馴染み深い量子力学の解釈です。
それは要約するならば、次のようなことを言っていました。
「物事の状態は観測されるまで決定されることがない」
※こちらの記事は2020年に配信されたものを大幅に改訂して再配信しています。
続き:歴史で学ぶ量子力学【新装版・4】は2022年1月3日18時公開
参考文献
量子革命: アインシュタインとボーア、偉大なる頭脳の激突 (新潮文庫)
