ホーキング定理が50年を経て実証される「ブラックホール合体後に表面積増大」

全ての画像を見る

宇宙でも非常に特殊な天体ブラックホール。

ブラックホールは観測が難しいですが、理論物理学者たちのインスピレーションの源泉ともなっていて、その性質についてさまざま予想が発表されています。

その中でも有名なものが、ホーキングとベッケンシュタインが予想した「ブラックホールはエントロピーを持っていて、それはブラックホールの表面積に保存されている」というものです。

この理論は2つのブラックホールが合体した場合、その表面積が元の2つのブラックホールの和より大きくなるということを予想していましたが、これを確認することは極めて困難だと考えられていました。

しかし、7月1日に科学雑誌『Physical Review Letters』に発表された新しい研究は、重力波観測の分析からホーキング・ベッケンシュタインの予想が事実であったことを確認したと報告しています。

すでに何をいっているのかわけがわからないという人が大多数でしょうが、今回はこの発見について解説していきます。

 

ブラックホールに物質が飲み込まれると宇宙のエントロピーは下がる？

まず今回の話を理解するために、エントロピーについて知っておきましょう。

エントロピーとは、日本語ではよく「煩雑さ」と訳されます。

「煩雑さ」といわれてもイマイチぴんと来ませんが、これは時間が経つと部屋が散らかるといっているのと同じ意味です。

もう少し厳密に表現すると、世界は自然のままに放っておくと「秩序から無秩序に向かっていく」ということを意味します。

そして、無秩序に再び秩序を与えるためには、エネルギーを消費して仕事をしなければならないのです。

たとえば、あなたが部屋でダラダラと1カ月以上過ごした場合、その部屋はかなり散らかるでしょう。

これは放っておいてもきれいに整頓された部屋には戻りません。気合を入れて掃除という仕事をしなければならず、そのためにあなたかお母さんが多くのエネルギーを消費することになります。

そのため理系の人は、人生で必ず一回は散らかった部屋を見て「部屋のエントロピーが増大している」という冗談をいいます。

では、物理学におけるエントロピーの増大とはなんなのでしょうか？　何が散らかるのでしょうか？

それはエネルギーです。

エネルギーとは熱であり、高温ほどエネルギーが高い状態を意味します。

温度が高いというのは、その場所にある分子の運動エネルギーが高いということです。

たとえば淹れたてのホットコーヒーは、液体の分子が高い運動エネルギーを持っています。

しかし、放っておけばコーヒーは冷めてしまいます。これは分子の運動エネルギーが部屋の中に散らばってしまうためです。

もとの熱いコーヒーに戻すには、ガスや電気を消費して、再び加熱しなければなりません。

電気代やガス代を消費せずに、コーヒーをもとの熱い状態に戻すことはできません。

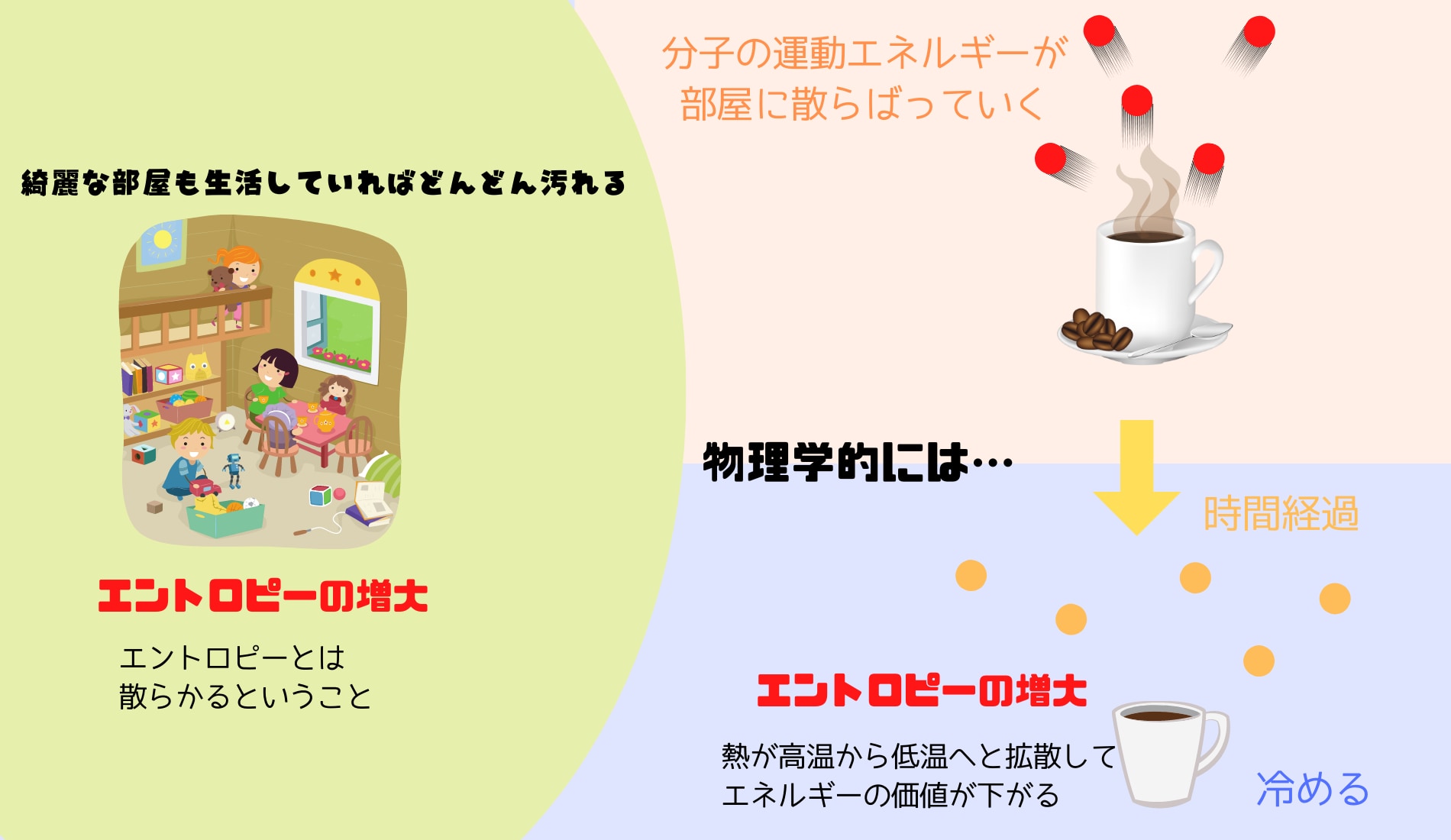
世界では秩序のある状態ほど価値が高いと見なすことができます。

つまりエントロピーの増大とは、ただ散らかすというだけでなく、世界はどんどん利用価値の低い状態に変わってしまうことを指しているのです。

こうした問題を、物理学では「エントロピーの増大則」または「熱力学第2法則」と呼びます。

これはもうちょっとネットで一般的な表現でいうなら「等価交換の原則」と言い換えることもできるでしょう。

無秩序に散らかった状態のものを秩序のある状態に戻すためには、他の秩序を持ったエネルギーを消費する（そちらを無秩序に変える）必要があるというわけです。

秩序の等価交換で、価値を保っているのが世界の原則なわけです。

ところが、広い宇宙を見渡したとき、こうした法則に従わずに済みそうな、ある特殊な存在が見つかりました。

それがブラックホールです。

ブラックホールはあらゆるものを吸い込んでしまい、1度事象の地平面の内側へ吸い込んだ物質は外へ逃しません。

エントロピーの増大した物質を飲み込んだら、その分のエントロピーは永遠に世界から失われることになってしまいます。

これはつまり、ブラックホールが世界のエントロピーを下げていることにならないだろうか？　というわけです。

ブラックホールはエントロピーを表面に溜め込んでいる？

こうした問題を解決するには、ブラックホールが何らかの方法で吸い込んだ物質のエントロピーを溜め込んでいると考える必要が出てきます。

しかし、ブラックホールはどうやってエントロピーを保存しているのでしょうか？

この問題を解決させるきっかけとなったのは、「ホーキングの面増大積則」です。

ホーキング博士はある夜、ブラックホールの表面となる事象の地平面がどうやって形成されるか考えていたとき、突然ブラックホールの表面積は増える一方で減ることはないはずだ、思いついたのです。

この考え聞いた、当時プリンストン大学の大学院生だったベッケンシュタインは、ブラックホールの表面積がある物理法則とそっくりであることに気が付きました。

それが「エントロピー増大則」です。

たしかに増える一方で減らないブラックホールの表面積と、増える一方で自然に減ることがないエントロピーは、多くの類似性を持っていました。

そこで、ベッケンシュタインはなんとブラックホールの表面積は、ブラックホールのエントロピーの尺度であるという考えを発表するのです。

ホーキング博士は最初、この大学院生のアイデアについて、自分の発見を勘違いしていると批判的だったようです。

しかし、ホーキング輻射という現象が理論的に発見されたことで、最終的にはベッケンシュタインの考え方は基本的には正しいということが認められたのです。

こうして、ブラックホールはエントロピーを持っていて、それは表面積に比例していると考えられるようになりました。

しかし、この考え方は非常に奇妙で不思議なものでした。

なぜなら、一般的に熱力学においてエントロピーという値は体積に比例するからです。

そして、これはもちろん理論的な予想に過ぎませんでした。

事実かどうかはわりません。これを物理学において事実と認めるためには、実際に観測して証拠を掴まなければならないのです。

物理学は世界を観る学問なので、頭の中で考えた理論予想だけでは、それがどれほどもっともらしい理屈でも絶対に認めることはありません。

では、どうすればこのことが事実だと観測で証明できるのでしょうか？

ここからが本題です。

合体したブラックホールの表面積はどうなる？

本題といいつつ、ここでもう一度、単純なたとえ話をしましょう。

私たちが部屋選びをするとき、広い部屋を借りようとすると、「いやいや、冬寒いよ」なんて意見を聞くことがあります。

広い部屋を暖房で温めることは、狭い部屋より大変だということは、別に物理学を学んでいなくても、誰でもすぐに理解できる問題です。

しかし、ここでは先程学んだエントロピーを使って、この問題を考えてみましょう。

温度は熱エネルギーであり、寒いということは熱エネルギーが低いということを意味します。

熱エネルギーが低い状態というのは、運動エネルギーが高い分子が散らばってしまい、無秩序な状態になっていることを意味します。

広い部屋と狭い部屋をイメージしたとき、狭い部屋なら熱い分子はあまり散らばらず、秩序をもたせやすいということが想像できます。

逆に広い部屋なら、熱い分子はあちこちに散らばって無秩序になってしまうでしょう。

つまり、広い部屋のほうがエントロピーが高いので、暖まりにくいと考えられるのです。

これはつまり、エントロピーという量は、体積に比例していると考えることができます。

では、ここでもう1つ、イメージを働かせてみましょう。

冬に旅館に泊まったときを想像してみてください。

その旅館の部屋は、食事をする居間と布団を敷いた寝室が襖で分けられています。居間と寝室は同じ広さの部屋です。

居間は暖房を効かせていてとても暖かくなっていますが、寝室は無人なので暖房をかけていませんでした。

このとき、「じゃあそろそろ寝ましょうか」と寝室の襖を開けると、部屋はどうなるでしょう？

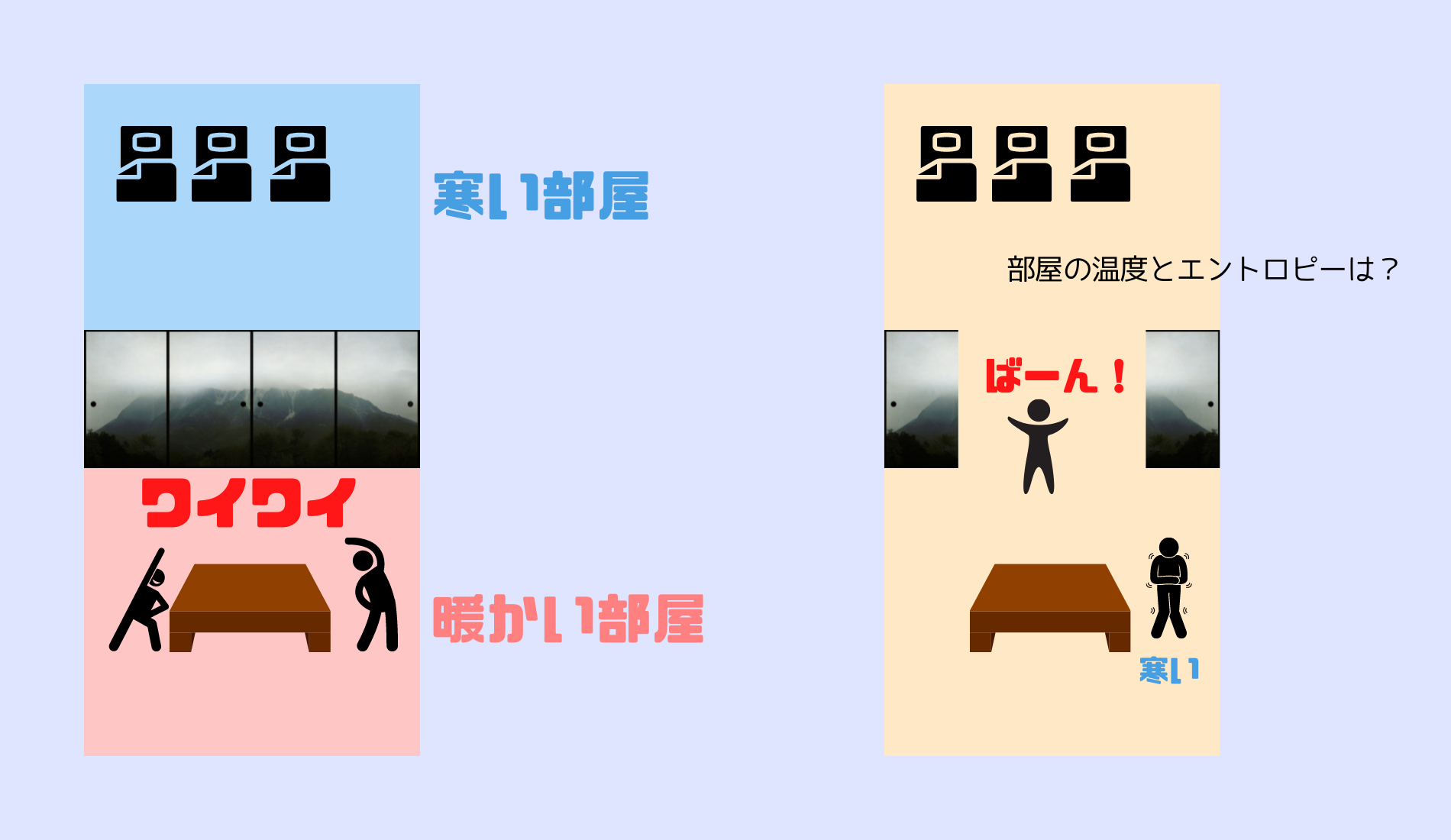
襖を開いたとき、部屋の体積は2倍に広がります。

暖かい空気は、冷たい寝室に流れ込み広がった空間に拡散して非常に混沌とした状態になります。

このとき部屋のエントロピーは、襖で仕切られていた狭い部屋がそれぞれ持っていたエントロピーの和よりも、もっとずっと高い状態になっているはずです。

ここが重要なポイントです。

エントロピーを持った個別の空間が合わさったとき、それは単純に両者の和にはならず、それよりも大きくなってしまうのです。

では今度こそ本題に入りましょう。

エントロピーを表面積として保存する2つのブラックホールが合体したとき、新しく生まれた融合ブラックホールの表面積はどうなると予想できるでしょうか？

そう、合体したブラックホールの表面積は、2つのブラックホールの表面積の和よりも大きくなってしまうと予想されるのです。

2つのブラックホールの合体を重力波で観測した

長々と語ってきましたが、今回の研究は、こうした出来事を、重力波望遠鏡を使って観測したのです。

観測されたのは「GW150914」というブラックホールで、これは太陽質量の29倍と36倍の2つのブラックホールが合体して誕生したものでした。

ブラックホールの合体という劇的な事象は、見えない時空の振動を引き起こします。

重力波観測は、2つの巨大な重力を持つ天体が合わさったときに発生する津波のような時空のゆらぎを観測するものです。

それははるか遠くの地球にもさざ波のようにして届きます。

そして、この重力波観測では、合体前の個別のブラックホールの重力波と合体したブラックホールの重力波を分けて詳細に分析することが可能です。

研究はこれをうまく選り分けで、それぞれのブラックホールの質量や回転速度（角運動量）を求めることに成功しました。

これらの情報を元に、研究チームは合体前のそれぞれのブラックホールの事象の地平面の表面積と、合体後の表面積を計算することができたのです。

結果、合体後のブラックホールの表面積は、合体前のブラックホールの表面積の和よりも大きいことが明らかとなったのです。

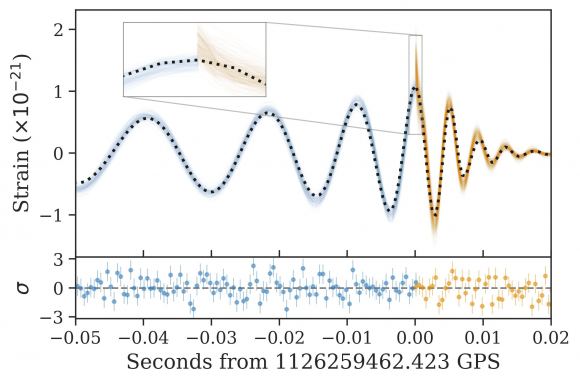
これはホーキングの面積定理と一致していました。

この観測の信頼性は最大97%であると、研究者は述べていて非常に長い時をかけて、ホーキング氏とベッケンシュタイン氏の予想が観測によって確認されたことになります。

ブラックホールの熱力学という難解な理論について、最初の証拠が提示されたのです。

これは物理学の大きな進展でしょう。

全ての画像を見る